![]() |
 

|
 |
![]()
![]() |
![]()
|
MATHEMATICAL MODELS. Conductor modelling
A transient temperature distribution in conductor components is described by a 1-D equation of heat balance with the transverse conductive and convective heat exchange and Joule heating terms. A temperature distribution across the conductor section is assumed to be uniform. Uniform temperature distribution is a "natural" assumption for a 1-D approach and treated as an average temperature for the given cross-section. In the general case, conductor could have simultaneously a contact with different helium flows as well as with other conductors. So the equation for a binary conductor m including the heat exchange with conductors n and helium flows i has a form:

where T, C, k, A1+A2 – conductor temperature, heat capacity, thermal conductivity and cross-section area of components accordingly; h, g –coefficient and perimeter of heat exchange; 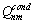 –conductive heat transfer from the conductors n and m per unit of length; –conductive heat transfer from the conductors n and m per unit of length; 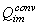 -convective heat transfer from
helium in the channel i to the
conductor m per unit of length; -convective heat transfer from
helium in the channel i to the
conductor m per unit of length;  - Joule heating of the conductor m per unit of length; - Joule heating of the conductor m per unit of length; 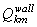 , kwall, Twall
- heat flux to the wall k, thermal conductivity and temperature of the wall k,
correspondingly; Iop -
conductor current; s - conductor electrical conductance; Ic, Tc, Tcs - critical current, critical temperature and current sharing temperature,
accordingly. , kwall, Twall
- heat flux to the wall k, thermal conductivity and temperature of the wall k,
correspondingly; Iop -
conductor current; s - conductor electrical conductance; Ic, Tc, Tcs - critical current, critical temperature and current sharing temperature,
accordingly.
In these equations the material cross-section Am is treated as the cross-section in a plane normal to the conductor axis ("twisted" cross-section). The same assumption is applied to the material heat exchange perimeter gm. It is taken that the "twisted" material cross-section and the perimeter (for twisted superconducting strands) used in the above equations are defined as Atw = Anon tw/cosq and gtw = gnon tw/cosq, where q>0 is an average twist angle. This generalized angle
takes into account the average twist of cabling stages. For non-twisted
materials cosq =1.
The following boundary conditions are used to
close equation (4). The temperatures at the ends of the conductor are defined
through temperature of connected joints by boundary condition of third kind

|
|
 |
![]()
 ![]() |
![]()
Germany (headquarters): Alphysica GmbH. Unterreut, 6, D-76135, Karlsruhe, Germany,
Phone: +49 (0)163 904-85-61,
Fax: +49 (0)7219 444-26-55, E-mail: info@alphysica.com
![]()
USA: Alphysica Inc. 414, Jackson street,
San Francisco, CA 94111, USA,
Phone/Fax: +1 415.230.23.63, E-mail:usa@alphysica.com
![]()
Russia: Alphysica Ltd. 55, ul. Mayakovskogo, 191025, St.Petersburg, Russia,
Phone/Fax: +7 (812) 335-95-04, E-mail: russia@alphysica.com
Copyright © 1994-2010
![]()
| |
|
![]() |



